Sous l'influence de la relativité générale

1991/10/01 Martin Axpe, Iñaki Iturria: Elhuyar aldizkaria

• Fisika

Quand Einstein a publié en 1905 la Théorie de la Relativité Spéciale (TUE), le concept que nous avions sur le temps est redevenu relatif. Dix ans plus tard, cependant, nous avons été encore plus surpris: l'espace et le temps que nous connaissons... sont courbes. Mais de quoi parlait quand il l'a courbé ?

Elhuyar. Science et Technique

face avant face avant

Dans le nombre, nous avons vu EBT. Alors nous avons dit que EBT ne sert que lorsque l'observateur se déplace à vitesse constante. Observateurs avec accélération

a) a)

En TC nous avons besoin d'une théorie plus générale, la théorie de la relativité générale (TCE). Cette théorie, en plus d'être plus rare que la TUE, exige une formulation mathématique plus difficile. Par conséquent, la règle et l'horloge

a) a)

vétéran

Malgré la simplicité de trouver des démonstrations de l'UET, les explications sur EOT sont beaucoup plus réduites. Dans tous les cas, nous essayerons de nous rapprocher avec attention du collectif de lecture pour ne pas chasser le lecteur

...

EBT et gravitation

Figure . Loi de gravitation de Newton (A) et TUE (B).

La gravitation, une loi qui explique l'attraction mutuelle des planètes (et de tous les corps de masse), a été conçue par Newton (voir figure 1-A), qui a servi à expliquer ce qui se voyait dans la pratique au cours des siècles… sauf quelques exceptions. Mais comme déjà commenté, la TUE exige une modification des formules, de sorte que la TUE oblige la formule traditionnelle à adopter la forme indiquée dans la figure 1-B. Cependant, les résultats de la nouvelle formule ne correspondent pas à l'expérience. Au contraire, ils sont encore pires que ceux de la formule ancienne.

Par conséquent, nous sommes arrivés à une situation où, d'une part, EBT ne sert pas pour les observateurs en accélération et, d'autre part, n'est pas en mesure d'expliquer la gravitation. Sur cette base, penser qu'il peut y avoir un certain rapport entre accélération et gravitation semble assez logique, et le travail d'Einstein a été de démontrer cette relation.

Espace/temps et TSE

Tous les événements se déroulent dans un lieu et un temps. Sans espace et sans temps il n'y a rien, rien n'est arrivé qui n'ait eu lieu nulle part ni à aucun moment avec clarté. L'espace/temps est donc la base, la structure ou l'emballage du monde.

Figure . Galileo nous a fait savoir que la plume et la brique tombent avec la même accélération (dans le vide, bien sûr, pour éviter la friction de l'air). Einstein nous a expliqué la raison : la nature de l'espace/temps.

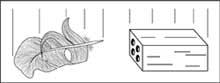
Il y a longtemps que tout le corps que Galilée avait cédé (aussi lourd que léger) tombait avec la même accélération était connu, mais il ne lui a pas donné d'importance.

Maintenant, pensons qu'un vélo qui parcourt la rue saute dans un endroit précis. Nous pensons que la cause peut être le vélo, le cycliste, la route ou le vent. Mais plus tard une voiture saute au même endroit, et il en va de même pour un bus et un camion. Une fois vu cela, nous dirons que la raison du saut n'a pas à voir avec les véhicules, mais avec la nature de la base, c'est-à-dire avec la route. Il en va de même pour Einstein, c'est-à-dire que la chute de tous les corps avec la même accélération est due à l'emballage, étant espace/temps (voir figure 2).

D'autre part, et puisque l'espace/temps est ou est indispensable pour que quelque chose se produise, l'espace/temps affecte tous les corps. Par conséquent, dans la nature il n'y a pas de fraction libre, et comme un observateur ou un corps doit être libre de circuler à vitesse constante, il n'y a pas d'observateurs inertiels (v=cte.) aussi. Par conséquent, il n'y a pas d'observateurs privilégiés. Tous les observateurs sont équivalents, c'est-à-dire que nous avons atteint une relativité totale, puisque nous n'avons plus à faire aucune restriction (TEE v=cte. nous avons demandé).

Figure . Si le bateau est accéléré, la balle est serrée contre le trottoir. Si nous la situons dans la zone de gravitation d'une planète, la balle est serrée contre le trottoir. L'observateur qui se trouve à l'intérieur du bateau ne pourra pas différencier les deux situations en serrant la balle.

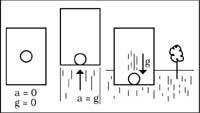
Par exemple, un astronaute crie dans l'espace et tombe contre un mur. Il ne sera pas possible pour l'homme de savoir si cette chute est due à l'inertie de l'accélération du navire ou à la gravitation d'une planète

Mais comment cette forme d'espace/temps est-elle formulée ? Et comment est-il lié aux mouvements des corps?

Caractéristiques spatio-temporelles

Figure . Espace bidimensionnel plat et incurvé. La launa n'influence pas le parcours de la balle. Kurbatua change le chemin de la balle.

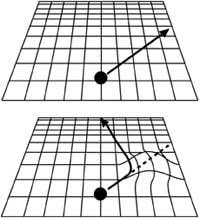
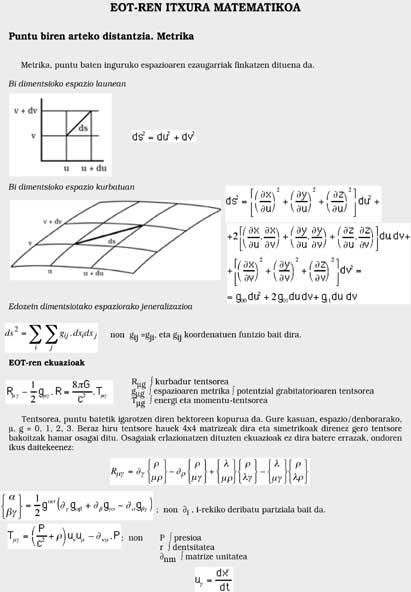
Auparavant, nous avons vu que la chute des corps est due à la forme spatiale/temporelle. Si cet espace/temps est plat il n'affectera pas. En cas de courbure, au contraire, cela affectera (voir figure 4). C'est pourquoi c'est notre espace/temps courbe. Malheureusement, il a quatre dimensions (trois pour l'espace et une pour le temps), donc nous ne pouvons pas voir cette courbure. Au contraire, les mathématiciens ne connaissent pas de frontières et expriment facilement la métrique spatio-temporelle. Ceux qui maîtrisent les mathématiques peuvent regarder le tableau, mais les autres mieux ne pas regarder.

Voyons maintenant la deuxième caractéristique. Dans les théories anciennes (y compris la TUE, et dans d'autres théories gravitationnelles actuelles), l'espace/temps était rigide, c'est-à-dire qu'il était un récipient d'événements, mais sans influencer les faits. Pour sa part, EOT revendique que l'espace/temps est aussi un objet dynamique, c'est-à-dire que les objets et événements déforment l'espace/temps et vice versa, les déformations spatio-temporelles affectent le comportement des objets et des événements (voir figure 5).

Figure . Dans les théories traditionnelles, l'espace/temps est rigide : rien n'affecte ni n'affecte rien. En revanche, EOT est déformé par l'incident.

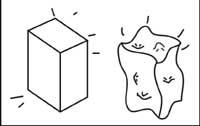
Par conséquent, en plus d'être un espace/temps courbe, il est également dynamique.

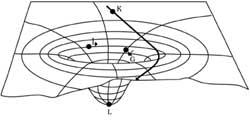
La dernière étape d'Einstein était d'identifier ces déformations avec la gravitation. Il a expliqué plus ou moins que jusqu'ici une masse attirait sans moyens ni ressources des objets de son environnement. Selon Eot, pour sa part, une masse déforme espace-temps et cette déformation conditionne les trajectoires des objets de son environnement (voir figure 6).

Il a donné à la théorie un reflet mathématique à travers plusieurs formules. Ces formules concernent la nature de l'espace/temps, la courbure, les masses et les énergies en jeu, mais elles sont si compliquées que je ne les mentionne que dans le tableau.

Conclusions

Figure . Influence d'une masse dans l'espace/temps. (L) La Terre courbe espace-temps et par conséquent (G) tombe vers la Terre, (I) la Lune tourne et (K) le parcours de la comète change.

Ces caractéristiques spatio-temporelles génèrent une série de conséquences. Les plus connus sont:

1. La trajectoire de la lumière est courbe quand elle passe par le côté d'une masse, car la lumière est également attirée par la gravitation (comme on peut le voir dans les Figures 6 et 7).
2. Plus l'enregistrement est grand, plus les montres vont lentement.
3. Il faut créer des ondes gravitationnelles comme celles qui apparaissent dans l'eau. ( Nous avons besoin de vous parce que vous n'avez pas encore trouvé).
4. La conséquence la plus connue est le trou le plus noir. Nous allons donc les analyser plus lentement.

Trous noirs

Figure . Courbure de la lumière dans un monde de grand G. Une personne qui regarde la télévision entend que quelqu'un est sur le point d'entrer dans le salon. Il pense être estrovil avec le camion. Mais l'autre entre et passe par le camion sans faire de strophes. Et c'est que le camion est derrière la télévision, devant la porte avec la courbure de l'image provoquée par la masse de la télévision.

Lorsque les équations d'Einstein ont été résolues,

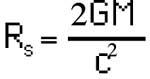
On constate l'absence de résolution des valeurs. Qu'est-ce qui se passait à cette distance? Au début, on a pensé que le corps ne pouvait pas être inférieur à cette mesure, mais ensuite on a montré qu'une étoile pouvait se contracter jusqu'à une taille inférieure à cette valeur. Alors on a _compris quels démons était R s, une limite. Tout (même la lumière elle-même) qui se trouve à une distance inférieure de R _s d'un corps ne pourra s'échapper et tombera sur le corps. Mais comme la lumière n'est pas capable d'échapper, nous ne pouvons pas voir ce corps. C'est pourquoi on l'appelle trou noir.

Exposition à ETAP

Que se passerait-il si notre Soleil (R _s) était capable d'atteindre cette mesure ? (En principe, la masse est insuffisante pour y parvenir). Au début, il serait contracté, de plus en plus petit. Plus tard, à mesure qu'il diminue, sa couleur devient de plus en plus rouge et finalement disparaît. Par conséquent, les planètes tourneraient autour de l'insignifiant. De rien ? Non, nous ne verrions pas le Soleil, mais sa masse serait enveloppée dans un point. Comme nous nous approchons de ce point nous ne le verrions pas, mais si nous nous approchons de 3 km (parce que R _s = 3 km pour le soleil) nous ne pourrions pas revenir en arrière. Une fois les 3 km dépassés, nous aussi (comme la lumière) resterions captifs et nous tirerions sur le point.

Pour détecter la densité nécessaire pour créer des trous noirs, rappelez-vous les données suivantes: Le R _s de la Terre est de 1 cm, c'est-à-dire si toute la Terre était contractée jusqu'à une sphère de moins de 1 cm de rayon, nous ne pourrions pas en sortir ni nous voir de l'extérieur. Ou en d'autres termes, notre Terre devrait l'attraper jusqu'à 1 cm pour devenir un trou noir.

Attention, cependant, avec les voyages: notre corps n'aurait rien à voir ou à percevoir parce qu'il survivrait assez.

Fou dans le monde

Cette courbure provoquée par les masses est due au fait que la valeur G est extrêmement faible (G = ^6,672 x 10 -11). Mais que se passerait-il si cette valeur était beaucoup plus grande ? Pour commencer, nous ne pourrions pas vivre sur Terre. Sa force d'attraction serait si grande qu'il nous piétinerait contre le trottoir. Les étoiles n'éclaireraient pas non plus le ciel comme une saucisse, car la plupart d'entre elles seraient des trous noirs. Tous les corps que nous verrions seraient rougeâtres. Et c'est que ce petit monde de G ressemblerait quand vous éclairez une pièce avec des ampoules rouges.

Dans ce cas aussi, pour différentes raisons, le paradoxe des jumeaux se produirait. Si le jour de Biki, deux naissances, nous portions l'un d'eux à la côte et l'autre à un sommet, en remontant au fil du temps, nous vérifierions que le premier serait jeune et le second aîné.

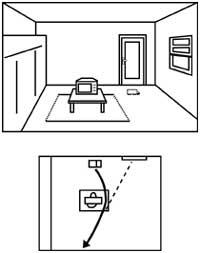
En outre, nous aurions une énorme difficulté à déterminer l'emplacement des objets en fonction de notre position (voir figure 7).

Et de tout cela, à la fin quoi ?

Ces exemples possibles peuvent être très bien, mais au quotidien nous ne percevons pas du tout les curiosités d'EBT et d'EOT, ni le temps relatif ni l'espace/temps courbe. Et la vérité est que même si la théorie a de nombreuses applications scientifiques, il n'y a pas de grandes erreurs à croire que le monde que nous voyons est comme ce que nous savons.

Oui, mais nous ne pouvons pas non plus rompre la curiosité, nous ne pouvons pas satisfaire la faim de la cause. Toute étape qui nous aidera à mettre en évidence les lois occultes du fonctionnement du monde sera passionnante. Et c'est que les fantasmes de l'ésotérisme sont pâles devant l'ET. Encore une fois, la réalité a dépassé la fiction.

(Note: Pour bien voir ces deux dernières images, vous pouvez aller au pdf).