Bajo la influencia de la relatividad general

1991/10/01 Martin Axpe, Iñaki Iturria: Elhuyar aldizkaria

• Fisika

Cuando Einstein publicó en 1905 la Teoría de la Relatividad Especial (TUE), el concepto que teníamos sobre el tiempo volvió a ser relativo. Diez años después, sin embargo, nos sorprendió aún más: el espacio y el tiempo que conocemos... son curvos. ¿Pero de qué hablaba cuando le curvó?

Elhuyar. Ciencia y Técnica

frente

En el número de, vimos EBT. Entonces dijimos que EBT sólo sirve cuando el observador se mueve a velocidad constante. Observadores con aceleración

a)

en TC necesitamos una teoría más general, la Teoría de la Relatividad General (TCE). Esta teoría, además de ser más rara que la TUE, requiere una formulación matemática más difícil. Por ello, la regla y el reloj

a)

veterano

A pesar de la sencillez de encontrar demostraciones de la UET, las explicaciones sobre EOT son mucho más reducidas. En cualquier caso, trataremos de acercarse con atención al colectivo de lectura para no ahuyentar al lector

...

EBT y gravitación

La gravitación, una ley que explica la atracción mutua de los planetas (y de todos los cuerpos con masa), fue ideada por Newton (ver figura 1-A), que sirvió para explicar lo que se veía en la práctica a lo largo de los siglos… salvo algunas excepciones. Pero como ya se comentó, la TUE exige una modificación de las fórmulas, por lo que la TUE obliga a que la fórmula tradicional adopte la forma indicada en la figura 1-B. Sin embargo, los resultados de la nueva fórmula no coinciden con la experiencia. Por el contrario, son aún peores que los de la fórmula antigua.

Por ello, hemos llegado a una situación en la que, por un lado, EBT no sirve para los observadores en aceleración y, por otro, no es capaz de explicar la gravitación. En base a esto, pensar que puede existir cierta relación entre aceleración y gravitación parece bastante lógico, y el trabajo de Einstein fue demostrar esa relación.

Espacio/tiempo y TSE

Todos los eventos se realizan en un lugar y tiempo. Sin espacio y sin tiempo no hay nada, no ha ocurrido nada que no haya ocurrido en ningún sitio ni en ningún momento con claridad. El espacio/tiempo es, por tanto, la base, estructura o envase del mundo.

Hace tiempo que todo el cuerpo que Galileo había cedido (tanto pesado como ligero) caía con la misma aceleración era conocido, pero no le dio importancia.

Ahora pensemos que una bicicleta que recorre la calle salta en un lugar concreto. Pensaremos que la causa puede ser la bicicleta, el ciclista, la carretera o el viento. Pero más tarde un coche salta en el mismo lugar, y lo mismo le pasa a un autobús y a un camión. Una vez visto esto, diremos que la razón del salto no tiene que ver con los vehículos, sino con la naturaleza de la base, es decir, con la carretera. Lo mismo dijo Einstein, es decir, que la caída de todos los cuerpos con la misma aceleración se debe al envase, al ser espacio/tiempo (ver figura 2).

Por otro lado, y dado que el espacio/tiempo es o es imprescindible para que ocurra algo, el espacio/tiempo afecta a todos los cuerpos. Por tanto, en la naturaleza no hay fracción libre, y como un observador o un cuerpo debe ser libre para circular a velocidad constante, no hay observadores inerciales (v=cte.) también. En consecuencia, no hay observadores privilegiados. Todos los observadores son equivalentes, es decir, hemos alcanzado una relatividad total, ya que ya no tenemos que hacer ninguna restricción (TEE v=cte. nos solicitaba).

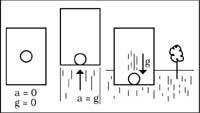
Por ejemplo, un astronauta grita en el espacio y cae contra una pared. No será posible que el hombre sepa si esta caída se debe a la inercia de la aceleración del buque o a la gravitación de un planeta

¿Pero cómo se formula esta forma de ser espacio/tiempo? ¿Y cómo se relaciona con los movimientos de los cuerpos?

Características espacio-temporales

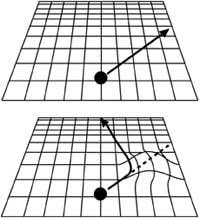
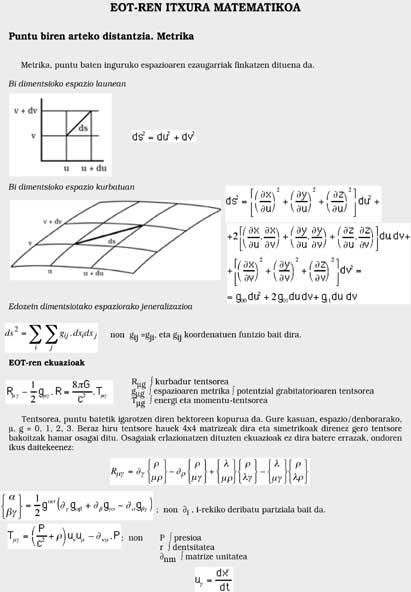
Antes hemos visto que la caída de los cuerpos se debe a la forma espacial/temporal. Si este espacio/tiempo es llano no afectará. En caso de ser curvado, por el contrario, afectará (ver figura 4). Por ello, es nuestro espacio/tiempo curvo. Lamentablemente tiene cuatro dimensiones (tres para el espacio y otra para el tiempo), por lo que no podemos ver esa curvatura. Por el contrario, los matemáticos no conocen fronteras y expresan la métrica espacio-temporal con total facilidad. Los que dominan las matemáticas pueden mirar al cuadro, pero los demás mejor no mirar.

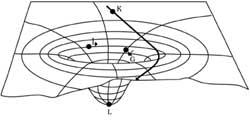
Veamos ahora la segunda característica. En las teorías antiguas (incluida la TUE, y en otras teorías gravitatorias actuales), el espacio/tiempo era rígido, es decir, era un recipiente de sucesos, pero sin influir en los hechos. Por su parte, EOT reivindica que el espacio/tiempo también es un objeto dinámico, es decir, que los objetos y sucesos deforman el espacio//tiempo y viceversa, las deformaciones espacio-temporales afectan al comportamiento de objetos y sucesos (ver figura 5).

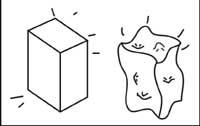
Por lo tanto, además de ser un espacio/tiempo curvo, también es dinámico.

El último paso de Einstein fue identificar estas deformaciones con la gravitación. Explicó más o menos que hasta ahora una masa atraía sin medios ni recursos a objetos de su entorno. Según Eot, por su parte, una masa deforma espacio-tiempo y esta deformación condiciona las trayectorias de los objetos de su entorno (ver figura 6).

Dio a la teoría un reflejo matemático a través de varias fórmulas. Estas fórmulas relacionan la naturaleza del espacio/tiempo, la curvatura y las masas y energías en juego, pero son tan complicadas que sólo las menciono en el cuadro.

Conclusiones

Estas características espacio-temporales generan una serie de consecuencias. Los más conocidos son:

1. La trayectoria de la luz se curva cuando pasa por el lateral de una masa, ya que la luz también es atraída por la gravitación (como se puede observar en las Figuras 6 y 7).
2. Cuanto más grande es la grabación, más lento van los relojes.
3. Hay que crear ondas gravitatorias como las que aparecen en el agua. ( Le necesitamos porque todavía no se han encontrado).
4. La consecuencia más conocida es el agujero más negro. Así que vamos a analizarlos más despacio.

Agujeros negros

Cuando se resolvieron por primera vez las ecuaciones de Einstein,

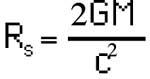
Se constata la ausencia de resolución de valores. ¿Qué pasaba a esa distancia? En un principio se pensó que el cuerpo no podía ser menor de esta medida, pero luego se demostró que una estrella podía contraerse hasta un tamaño menor que ese valor. Entonces se entendió _qué demontres era R s, un límite. Cualquier cosa (incluso la propia luz) que se encuentre a una distancia menor de R _s de un cuerpo no podrá escapar y se caerá contra el cuerpo. Pero como la luz tampoco es capaz de escapar, nosotros no podremos ver ese cuerpo. Por eso se llama agujero negro.

Exposición a ETAP

¿Qué pasaría si nuestro Sol (R _s) fuera capaz de alcanzar esta medida? (En principio la masa es insuficiente para conseguirlo). En un principio se vería contraído, cada vez más pequeño. Posteriormente, a medida que se vaya reduciendo, su color se haría cada vez más rojo y finalmente desaparecería. Por lo tanto, los planetas girarían alrededor de lo insignificante. ¿De nada? No, nosotros no veríamos el Sol, pero su masa estaría envuelta en un punto. A medida que nos acercamos a este punto no lo veríamos, pero si nos acercamos a 3 km (porque R _s = 3 km para el Sol) no podríamos volver atrás. Una vez superados los 3 km, nosotros también (como la luz) nos quedaríamos cautivos y tiraríamos contra el punto.

Para detectar la densidad necesaria para crear agujeros negros, recuerda el siguiente dato: El R _s de la Tierra es de 1 cm, es decir, si toda la Tierra estuviera contraída hasta una esfera de menos de 1 cm de radio, no podríamos salir de ella ni nos verían desde fuera. O en otras palabras, nuestra Tierra debería contraerla hasta 1 cm para convertirse en un agujero negro.

Cuidado, sin embargo, con los viajes: nuestro cuerpo no tendría nada que ver o percibir porque sobreviviría lo suficiente.

Loco en el mundo

Esta curvatura provocada por las masas se debe a que el valor G es extremadamente bajo (G = ^6,672 x 10 -11). ¿Pero qué pasaría si ese valor fuera mucho mayor? Para empezar, no podríamos vivir en la Tierra. Su fuerza de atracción sería tan grande que nos pisaría contra el pavimento. Las estrellas tampoco iluminarían el cielo como salpicón, ya que la mayoría de ellas serían agujeros negros. Todos los cuerpos que veríamos serían rojizos. Y es que este mundo de G pequeño se vería como cuando iluminas una habitación con bombillas rojas.

También en este caso, por diferentes motivos, se produciría la paradoja de los gemelos. Si el día de Biki, dos nacidos, lleváramos uno de ellos a la costa y el otro a una cima, volviendo a juntarnos con el paso del tiempo, comprobaríamos que el primero sería joven y el segundo anciano.

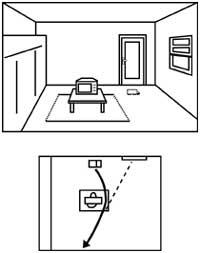
Además, tendríamos una enorme dificultad para determinar la ubicación de los objetos en función de nuestra posición (ver figura 7).

Y de todo esto, ¿al final qué?

Estos posibles ejemplos pueden estar muy bien, pero en el día a día no percibimos en absoluto las curiosidades de EBT y EOT, ni el tiempo relativo ni el espacio/tiempo curvo. Y la verdad es que aunque la teoría tiene muchas aplicaciones científicas, no hay grandes errores en creer que el mundo que vemos es como lo que sabemos.

Sí, pero nosotros tampoco podemos romper la curiosidad, no podemos satisfacer el hambre de la causa. Cualquier paso que nos ayude a poner en evidencia las leyes ocultas que tiene el funcionamiento del mundo resultará apasionante. Y es que las fantasías del esoterismo quedan pálidas ante la ET. Una vez más, la realidad ha superado la ficción.

(Nota: Para ver bien estas dos últimas imágenes puedes ir al pdf).