Under the influence of general relativity

1991/10/01 Martin Axpe, Iñaki Iturria: Elhuyar aldizkaria

• Fisika

When Einstein published in 1905 the Theory of Special Relativity (TUE), the concept we had about time became relative again. Ten years later, however, we were even more surprised: the space and time we know... are curved. But what did he talk about when he bent him?

Elhuyar. Science and Technology

front

In the number of, we saw EBT. Then we said that EBT only serves when the observer moves at constant speed. Observers with acceleration

a)

in TC we need a more general theory, the Theory of General Relativity (TCE). This theory, in addition to being more rare than TEU, requires a more difficult mathematical formulation. Therefore, the rule and the clock

a)

veteran

Despite the simplicity of finding UET demonstrations, explanations about EOT are much smaller. In any case, we will try to approach with attention the reading collective so as not to chase away the reader

...

EBT and gravitation

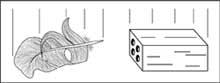
Gravitation, a law that explains the mutual attraction of planets (and all bodies with mass), was devised by Newton (see Figure 1-A), which served to explain what was seen in practice over the centuries… except for some exceptions. But as already mentioned, the TUE requires a modification of the formulas, so the TUE requires that the traditional formula adopt the form indicated in figure 1-B. However, the results of the new formula do not match the experience. On the contrary, they are even worse than those of the old formula.

For this reason, we have come to a situation in which, on the one hand, EBT does not serve for accelerating observers and, on the other, it is not able to explain gravitation. Based on this, thinking that there may be a certain relationship between acceleration and gravitation seems quite logical, and Einstein's work was to demonstrate that relationship.

Space/time and TSE

All events are held in one place and time. Without space and without time there is nothing, nothing has happened that has not happened anywhere or at any time clearly. Space/time is therefore the foundation, structure or container of the world.

Long ago the whole body that Galileo had yielded (both heavy and light) fell with the same acceleration was known, but it did not matter to him.

Now let's think that a bicycle that runs along the street jumps in a specific place. We will think that the cause can be the bicycle, the cyclist, the road or the wind. But later a car jumps in the same place, and the same happens to a bus and a truck. Once we have seen this, we will say that the reason for the jump has nothing to do with the vehicles, but with the nature of the base, that is, with the road. Einstein said the same, that is, that the fall of all bodies with the same acceleration is due to the container, being space/time (see figure 2).

On the other hand, and since space/time is or is essential for something to happen, space/time affects all bodies. Therefore, in nature there is no free fraction, and as an observer or a body must be free to circulate at constant speed, there are no inertial observers (v=cte.) also. Consequently, there are no privileged observers. All observers are equivalent, that is, we have reached a total relativity, since we no longer have to make any restrictions (TEE v=cte. requested us).

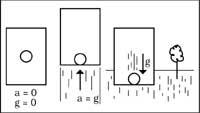
For example, an astronaut screams in space and falls against a wall. It will not be possible for man to know if this fall is due to the inertia of the acceleration of the ship or the gravitation of a planet

But how is this way of being space/time formulated? And how does it relate to body movements?

Space-time features

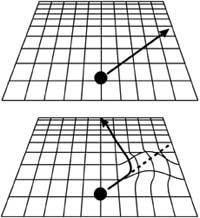
We have seen before that the fall of the bodies is due to the spatial/temporal form. If this space/time is flat it will not affect. In case of bending, on the contrary, it will affect (see figure 4). Therefore, it is our curved space/time. Unfortunately it has four dimensions (three for space and one for time), so we cannot see that curvature. On the contrary, mathematicians do not know borders and express space-time metrics with complete ease. Those who master mathematics can look at the picture, but others better not look.

Let us now see the second feature. In ancient theories (including the TEU, and in other current gravitational theories), space/time was rigid, that is, it was a vessel of events, but without influencing the facts. For its part, EOT claims that space/time is also a dynamic object, that is, that objects and events deform space/time and vice versa, space-time deformations affect the behavior of objects and events (see figure 5).

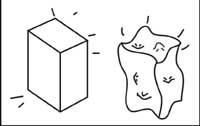
Therefore, besides being a curved space/time, it is also dynamic.

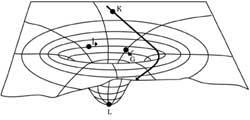
Einstein's last step was to identify these deformations with gravitation. He explained more or less that until now a mass attracted objects from its surroundings without means or resources. According to Eot, for his part, a mass deforms space-time and this deformation conditions the trajectories of the objects of his environment (see figure 6).

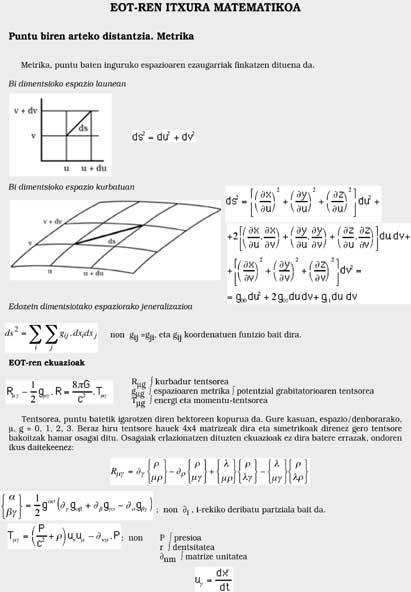
He gave the theory a mathematical reflection through various formulas. These formulas relate the nature of space/time, the curvature and the masses and energies at stake, but they are so complicated that I only mention them in the picture.

Conclusions

These spatio-temporal characteristics generate a series of consequences. The best known are:

1. The path of light curves when it passes through the side of a mass, since light is also attracted by gravitation (as can be seen in Figures 6 and 7).
2. The bigger the recording, the slower the clocks go.
3. You have to create gravitational waves like those that appear in the water. ("We need him because they have not yet been found.")
4. The most known consequence is the blackest hole. So let's analyze them more slowly.

Black holes

When Einstein's equations were first resolved,

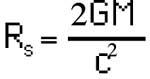
We note the absence of resolution of values. What happened at that distance? At first it was thought that the body could not be less than this measure, but then it was shown that a star could contract up to a smaller size than that value. Then it was _understood what demontres was R s, a limit. Anything (even the light itself) that is at a lesser distance from R _s of a body cannot escape and fall against the body. But since light is not able to escape either, we cannot see that body. That's why it's called a black hole.

Exposure to TAP

What if our Sun (R's) _were able to achieve this measure? (In principle the mass is insufficient to achieve it). At first it would be contracted, smaller and smaller. Later, as it shrinks, its color would become increasingly red and eventually disappear. Therefore, the planets would revolve around the insignificant. Nothing? No, we would not see the Sun, but its mass would be wrapped in one point. As we approached this point we would not see it, but if we approached 3 km (because R _s = 3 km for the Sun) we could not go back. Once exceeded 3 km, we too (like the light) would remain captive and throw against the point.

To detect the density needed to create black holes, remember the following data: The R _s of the Earth is 1 cm, that is, if the whole Earth were contracted to a sphere of less than 1 cm of radius, we could not leave it or see us from outside. Or in other words, our Earth should contract it up to 1 cm to become a black hole.

Be careful, however, with travel: our body would have nothing to do with or perceive because it would survive long enough.

Crazy in the world

This curvature caused by the masses is because the G value is extremely low (G = ^6,672 x 10 -11). But what if that value were much greater? To begin with, we could not live on Earth. His pull would be so great that he would step against the pavement. The stars would not illuminate the sky like a splash either, since most of them would be black holes. All the bodies we would see would be reddish. And this little G world would look like when you lit a room with red bulbs.

Also in this case, for different reasons, the paradox of the twins would occur. If the day of Biki, two born, we took one of them to the coast and the other to a summit, returning to join us with the passage of time, we would see that the first would be young and the second old.

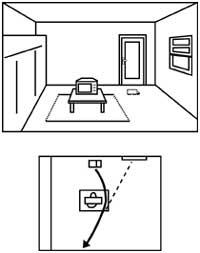
In addition, we would have a huge difficulty in determining the location of objects based on our position (see figure 7).

And of all this, in the end what?

These possible examples may be very good, but in everyday life we do not perceive at all the curiosities of EBT and EOT, neither the relative time nor the curved space/time. And the truth is that although theory has many scientific applications, there are no big mistakes in believing that the world we see is like what we know.

Yes, but we cannot break curiosity either, we cannot satisfy the hunger of the cause. Any step that helps us to expose the hidden laws of the workings of the world will be exciting. And the fantasies of esotericism are pale before the ET. Once again, reality has surpassed fiction.

(Note: To see these last two images you can go to the pdf).