Cows of Archimedes
1994/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
But his hobby did not refer to deep mathematical problems. On the contrary, Archimedes also addressed the PLAYFUL aspect of mathematics. An example of this is the problem of cows.
Classical mathematics left us problems of difficult resolution (circle square, angle trisection, Fermat theorems,...). With new ideas or ingenious reasoning many of them have been resolved or proved insoluble. Others, however, still await response. It is surprising that among so many problems, Archimedes' problems only need calculations. To be able to do these calculations have had to spend 2000 years. They were calculations so heavy that only the computer could resist.
BC. III. We are in the twentieth century, Archimedes has given an approximation to the number:
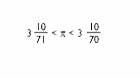
The Apollonius Key, in addition to offering a better approximation, has criticized Archimedes' work in the treatise on the multiplication of large numbers. Archimedes, overwhelmed by previous facts, prepares revenge by inventing and sending a difficult problem that needs large numbers, which dominates its competitors. Apollonius' answer is unknown, but he has also sent the problem to Eratosthenes, the librarian of Alexandria, and thanks to it has reached our hands.
All this is legend and we do not know whether it is true or not. On the other hand, the problem is at least that of C. II. It is also admitted that he is a subordinate and that the numbers to be used to solve are truly great. The smallest solution, for example, has 206,545 figures.
The complete statement of the problem was discovered in 1773 by Gotthold Ephraim Lessing in a Wolfenbüttel library. It was written in Greek and consisted of paired lines. The summary may be as follows:
Calculate, friend, the number of solar cattle. Think about it if you have knowledge. It calculates once the number of people staying in the Sicilian plains, divided by colors into four groups: one white, another black, another red and the last pinto. The bulls were more than cows, under the following conditions:
1. White bulls = red bulls + (1/2 + 1/3) black bulls.
2. Black bulls = red bulls + (1/4 + 1/5) painted bulls.
3. Pintos bulls = red bulls + (1/6 + 1/7) white bulls.
4º White cows = (1/3 + 1/4) black balance.
5. Black cows = (1/4 + 1/5) painted balance.
6th pint cows = (1/5 + 1/6) red balance.
7. Red cows = (1/6 + 1/7) white balance.
If you can donate the number of cattle and cows for each balance, friend, you have no match between the numbers. But you still cannot be part of the group of sages. To do this, you must take into account the following relationships between the solar reses:
8th. White bulls + black bulls = all square (p2).
9. Red bulls + red bulls = triangular number (n(n+1)/2).
When you calculate the entire balance, then, friend, register in full right and presume that your name shines in the world of knowledge.
As you can see, two problems appear in one. The first seven conditions are easy to solve. However, the nine have created difficulties for 2,000 years.
Keep in mind that both accept infinite solutions. The problem is to find the smallest solution. Performing algebraic operations will allow obtaining the following results:
White bulls = 10 366 482 K Black bulls
= 7 460 514 K Pint bulls
= 7 358 060 K Red bulls
= 4 149 387 K White cows
= 7 206 360 K Black cows
= 4 893 246 K Pint cows
= 3 515 820 K Red cows
= 5 439 213 K
In the above results K is any natural number. Giving values to K different solutions are obtained. The smallest solution is obtained by making K = 1. In this case the total number of animals is 50 389 082.
As for the second problem, it seems that at the time of Archimedes there were no tools to solve. Until 100 years ago, no progress was made. In 1880 A. The German Amthor made equations more useful and said that the solution began with 776 .. and had 206,542 figures. He succeeded in the first, but in the second he was wrong with 3 figures.
The first error-free solution was obtained in 1965 using a computer, but it was not published anywhere. Authors of the H.C. Willians, S.A. German and C.R. This is the Canadian zarnques. In 1981 Harry L. American Nelson used the problem to test the CRAY-1 computer. He obtained the solution in 10 minutes and printed it in 47 pages. The 47 pages are in number 3 of volume 13 of the journal “Journal of Recreational Mathematics”.
Why are the first and second problem solutions so different? Meeting condition 8 is not so difficult. Black and white bulls total 17 826 996 K. Therefore, taking K = 17 826 996, we get the full square. Difficulty arises when considering condition 9.
Condition 8 can be written as:
p 2 = 17 826 996 K
= 4 . 4 456 749 K;
Now, choosing K = 4 456 749 t 2 and replacing it in the previous equality, you get:
p 2 = 4 . 4 456 749 4 456 749 t 2
= 2 . (4 456 749)2 . 2
= (2) 4 456 749 t.
that is, we have the whole square. That is the progress Amthon achieved. Thus, if K = 4 456 749 t2 is selected, the condition 9 can be written as:
Red bulls + red bulls = 51 285 802 909 803 . considering that t 2
51 285 802 909 803 t 2 = n (n+1) / 2
n, being t natural numbers.
(We recommend that the reader not seek the solution of the above equality.)
Those who used the Archimedes problem to test the CRAY-1 were unhappy with the first solution and began to look for the next five. The largest of these five figures exceeds one million euros. Good balance!
Our question is how could you live so much cattle in Sicily?
Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia
