2006ko Abel saria: analista baten indarra

1902an, hiru asmo agertu ziren Niels Henrik Abelen jaiotzaren lehen mendeurrena ospatzeko eta haren izen handia zabaltzeko: kultura-ekitaldiak egitea, estatua bat jartzea eta nazioarteko sari bat antolatzea. Kultura- ekitaldiak egin ziren, estatua 1908an inauguratu zuten, baina saria ez zuten antolatu. Egitekotan egon omen ziren, baina 1905ean Norvegia Suediatik banandu zenean, han joan ziren saria eratzeko ametsak.

Bigarren mendeurrena betetzear zela, ehun urte lehenagoko ideia berreskuratu eta Norvegiako gobernuari saria sortzeko eskatu zioten. Herri barruko eta atzerriko sostengu ugari izan zituen asmoak eta 2002an Norvegiako gobernuak Abel Funtsaren estatutuak onartu zituen. Funtsaren helburu nagusia da "Matematikaren arloko lan zientifiko nabarmen bati nazioarteko sari bat ematea". Badirudi sari hau Matematikako Nobel saria izan zitekeenaren ordezkoa izateko bidean egon daitekeela: non ematen den --Norvegian--, nork --Norvegiako errege edo erreginak--, zenbat diru --ia Nobelak beste--. Hala den edo ez geroak esango du, sariak urteak bete ahala.

Lennart Carleson

2006ko Abel sariduna Lennart Carleson izan da, analisi klasikoan nabarmendu den matematikaria. Stockholmen jaioa 1928an, Uppsalako Unibertsitatean ikasi zuen eta han aurkeztu zuen doktore-tesia 1950ean. Matematikak, analisiak batez ere, tradizio ederra izan du Suedian, XIX. mendeko bigarren erditik aurrera. Carlesonen zuzendari Arne Beurling bera analista aipagarria da.

Hogeita bost urterekin Stockholmeko Unibertsitateko irakasle-postua lortu zuen, baina berehala itzuli zen Uppsalara. Han 1993 arte izan zen irakasle; urte batzuk geroago lan hura utzi gabe, Los Angelesko UCLA unibertsitateko irakasle ere izan zen.

Carlesonen lanen artean nabarmentzekoak dira zenbait urtez ebazpenaren zain egon diren problema zailei eman dien erantzuna. Adibidez, 1962an Koroaren teorema frogatu zuen, eta, hala, Kakutani matematikari japoniarrak hogei urte lehenago plazaratutako galdera ebatzi zuen.

Handiagoa izan zen lau urte geroago egin zuena, Fourieren serieen teorian zegoen problema irekirik handiena argitu baitzuen, puntuz puntuko konbergentziarena. Horrekin Matematikaren historian sartu zen.

Gainera, 1980ko hamarkadan, matematikariek emaitza nagusiak gazterik lortzen dituztela dioen ustearen aurka, sistema dinamiko leunetan zebilen problema ireki bati erantzuna eman zion, Michael Benedicksekin batera.

Horretaz guztiaz gain, nabarmena da Carlesonek Matematikaren alde egin duen bestelako lana ere. Hona hemen adibide bat. 1916an Mittag-Leffler senar-emazteek beren etxea eta liburutegia Suediako Zientzia Akademiari uzteko asmoa adierazi zuten, matematika-institutu bat eratzeko. 1927an hil zen Mittag-Leffler, sortu zen institutua, baina ez zen antolatu hark izan zituen asmoen arabera, diru faltagatik. 1967an Suediako Gobernuak Carlesoni nahi zuen lekuan lan egiteko aukera eman zion eta hark Mittag-Leffler institutua martxan jartzea erabaki zuen. Baita egin ere; behar ziren diru-laguntzak lortu eta munduko ikerketa-zentro ospetsuenetakoa bilakarazi zuen. 1984ra arte institutuko zuzendaria izan zen.

Fourieren serieak

Berrehun urte betetzear dira Fourieren serieak. Izan ere, 1807koa da Joseph Fourierek Parisko Zientzia Akademiari aurkeztu zion lehen lana. Beroaren hedapenerako ekuazioa proposatu eta ebatzi zuen, horretarako beren-beregi bide bat asmatuz, hain erabilgarria suertatu den aldagai-banaketa, alegia. Hasierako tenperatura ematen duen funtzioa sinu eta kosinuen serie modura, hau da, batura infinitu modura idatzi behar da, eta hori funtzio guztietarako egin daitekeela baieztatu zuen Fourierek.

Baieztatu bai, frogatu ez. Ez da harritzekoa ere, ordura arte analisi matematikoak izugarri garatu baitzituen

kalkulu-tresnak, baina ez 'geometriaren erako frogabideak', Cauchy-ren hitzetan esateko. Zorroztasunaren haize berriak frogak eskatzen zituenez, Fourieren baieztapena teorema ez, baina problema bihurtu zen. Eta oso garrantzitsua, XIX. mendeko analisi matematikoaren kontzeptu askoren sorreran eta bilakaeran serie trigonometrikoak izan baitziren: funtzioa, integrala, konbergentzia uniformea...

XIX. mendeari agur esaterako, Fourieren serieen teoria klasikoa egina zegoen. XX. mendearen lehen urteetan, hala ere, erabat berritu zuten arloa. Bi izan ziren horren arrazoiak: Lebesgueren neurriaren eta integralaren teoria, eta funtzio-espazioen teoria, hots, gaur egungo analisi funtzionala.

1913an heldu zen Lusin-en aierua: funtzio baten karratua integragarria bada, haren Fourieren seriea funtzioarekin bat dator puntu guztietan, "zero luzera duen multzo batean" izan ezik, beharbada. Lusin matematikari errusiarrari zor diogu baieztapena, ez frogatua, baina bai teorema izateko uste sendoarekin plazaratua.

Urteak joan, urteak etorri, beste teorema batzuk bildu ziren Fourieren serieen alorrera, baina inork ez zion kategoria hori ematen Lusinen aieruari. Ezta aurkakoari ere, hori ere gerta zitekeen eta. Egia esan, une batetik aurrera adituen artean uste hori zabaltzen hasi zen, Lusinen intuizioa oker ibili zela. Horregatik, 1965ean Carlesonek teorema frogatu zuenean, sorpresa ere izan zen neurri batean.

Carlesonek berak kontatu du zenbait urtez aieruaren aurkakoa frogatzen saiatu zela. Kontradibide baterako tresna guztiak eskura zituela uste zuenean, ezinezkoa suertatu zitzaion. Orduan ikusi zuen argi beste bidea hartu behar zuela, baiezkoarena, eta metatutako tresnekin eskuratu ahal izan zuen emaitza.

Carlesonen frogak hasieratik izan zuen misteriotsu izatearen fama. Teknikoki zuzena zela ikusi arren, ez zen ulertzen. Oraindik ere badirudi haren barne-egituraren zergatiak maldatsuegiak direla gehienentzat. Michael Christ matematikariaren konparazioa erabiltzeko, zortzi mila metroko mendi baten igoeraren antzekoa da, gehienok ez gara gauza geure kabuz bidea egiteko, baina Carlesonek erakutsi zigun badela gailurrera daraman bide bat.

Sistema dinamikoak

Matematikaren beste arlo batean ere egin zituen Carlesonek gailurrerako bideak, esaterako, sistema dinamikoetan.

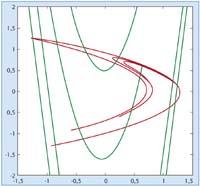
Hartu funtzio bat planotik planora, adibidez, eta puntu batean hasita aplikatu funtzioa behin eta berriro. Zein da lortzen den puntu-segidaren --orbitaren-- portaera? Limite baterantz hurbiltzen da, infiniturantz doa edo beste zerbait egiten du? Galdera horretatik abiatuta eta funtzioen arabera, Matematikaren alor bat sortu zen XIX. mendearen amaieran, Henri Poincaré matematikari frantsesaren eskutik, batez ere.

Emaitza teoriko batzuen ondotik, arloko benetako berrikuntza ordenagailuak ekarri zuen. Puntuen orbitak pantailan ikusaraziz, zer gerta zitekeen susmatzeko modua zegoen, aieruak egiteko, alegia. Gero frogek etorri beharko zuten. Hortik sortu zen Kaosaren teoria deitu duten hori.

Askotan aipatzen da Lorentz meteorologoaren azterketa bat kaosaren lehen adibideetako baten modura. 1976an beste meteorologo batek, Michel Hénonek, Lorentzen ekuazioak laburtuz planoko sistema bat eman zuen, non portaera berezi samarra agertzen den. Multzo 'arraro' bat atzematen da, orbitek harantz jotzen dute (multzora hurbiltzen dira baina ez balio zehatz batera), baina multzoko puntu batean hasiz gero multzoan bertan alderrai dabilen orbita lortzen da. Eta ez hori bakarrik, multzoaren egitura bera da arraroa, fraktala baita. Horregatik erakarle arraroa terminoa asmatu zen. Froga daiteke hori matematikoki?

1980ko hamarkadan sartu zen Carleson sistema dinamikoen arloan. Michael Benedicks-ekin batera, metodo berri bat asmatu zuen lehenengo kasu erraz bat aztertzeko. Ondoren, metodoa Hénonen sisteman aplikatu ahal izateko egokitu zuten eta haren dinamika deskribatzeko gauza izan ziren, zenbait urte lehenagoko aierua teorema bihurtuz. Emaitza horiek bilduz, Carlesonek eta Benedicksek 1992an argitaratu zuten artikulua mugarritzat gelditu da sistema dinamikoen teorian.